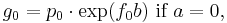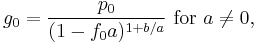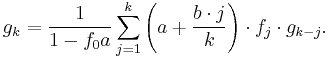Panjer recursion
The Panjer recursion is an algorithm to compute the probability distribution of a compound random variable
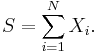 .
.
where both 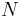 and
and 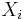 are random variables and of special types. In more general cases the distribution of S is a compound distribution. The recursion for the special cases considered was introduced in a paper of Harry Panjer[1]. It is heavily used in actuarial science.
are random variables and of special types. In more general cases the distribution of S is a compound distribution. The recursion for the special cases considered was introduced in a paper of Harry Panjer[1]. It is heavily used in actuarial science.
Contents |
Preliminaries
We are interested in the compound random variable 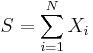 where
where 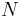 and
and 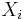 fulfill the following preconditions.
fulfill the following preconditions.
Claim size distribution
We assume the 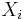 to be i.i.d. and independent of
to be i.i.d. and independent of 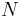 . Furthermore the
. Furthermore the 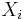 have to be distributed on a lattice
have to be distributed on a lattice 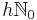 with latticewidth
with latticewidth 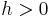 .
.
Claim number distribution
The number of claims N is a random variable, which is said to have a "claim number distribution", and which can take values 0, 1, 2, .... etc.. For the "Panjer recursion", the probability distribution of N has to be a member of the Panjer class, otherwise known as the (a,b,0) class of distributions. This class consists of all counting random variables which fulfill the following relation:
for some a and b which fulfill 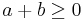 . The initial value
. The initial value  is determined such that
is determined such that 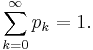
The Panjer recursion makes use of this iterative relationship to specify a recursive way of constructing the probability distribution of S. In the following  denotes the probability generating function of N: for this see the table in (a,b,0) class of distributions.
denotes the probability generating function of N: for this see the table in (a,b,0) class of distributions.
Recursion
The algorithm now gives a recursion to compute the ![g_k =P[S = hk] \,](/2012-wikipedia_en_all_nopic_01_2012/I/7e0c95c9662338046dda90176f9ad258.png) .
.
The starting value is 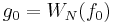 with the special cases
with the special cases
and
and proceed with
Example
The following example shows the approximated density of 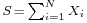 where
where 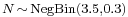 and
and 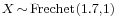 with lattice width h = 0.04. (See Fréchet distribution.)
with lattice width h = 0.04. (See Fréchet distribution.)
References
- ^ Panjer, Harry H. (1981). "Recursive evaluation of a family of compound distributions." (PDF). ASTIN Bulletin (International Actuarial Association) 12 (1): 22–26. http://www.casact.org/library/astin/vol12no1/22.pdf.
![f_k = P[X_i = hk].\,](/2012-wikipedia_en_all_nopic_01_2012/I/0aec4af2d75e9eb87a5091179a297b4a.png)
![P[N=k] = p_k= (a %2B \frac{b}{k}) \cdot p_{k-1},~~k \ge 1.\,](/2012-wikipedia_en_all_nopic_01_2012/I/8410ac49ee291dbbc206bca59999d6a3.png)